Review: Margins & Graph Design (Stata)

Margins

When we are talking about margins, we are really talking about two separate commands we can do within this one command: predicted values OR marginal effects. These two commands help us illustrate the effects that we have found in our model for our reader. It can help convey effect size or interactions. If you master the margins command, you can use it to highlight a particular finding for your reader. You can list the values or marginal effects as numbers or plot it. I will display each of the examples via plots.

What is a predicted value?
Remember, all the models we run are based on equations that are trying to predict our dependent variable (aka our outcome - Y). Once we run the model, we actually get an equation we can use. If we plug in specific values for our independent variables (our X's), then we can predict the value of our outcome. In a linear regression, that outcome is some continuous variable: income, years in the NBA, life expectancy, etc. In a regression with a binary outcome, the predicted value is actually a predicted probability. In a regression with a count outcome, the predicted value is, you guessed it, a count.

To get a predicted value out of the margins command, you don't have to add anything special! This is the default for the margins command.

What is a marginal effect?
A marginal effect tells us how much our outcome (Y) changes based on a one unit change in X. This hopefully sounds familiar to you. That's because it's how we interpret coefficients in a linear regression. Basically, a marginal effect is a slope. In a linear regression, the slope is constant. A one unit change in X causes the same change in Y for any X value. In other models, the slope changes as you go up the range of X. It's actually the instantaneous rate of change, meaning the slope at a particular point. This is harkening back to your calculus classes. In the image below, the dashed line shows you the slope at the point where the arrow ends.

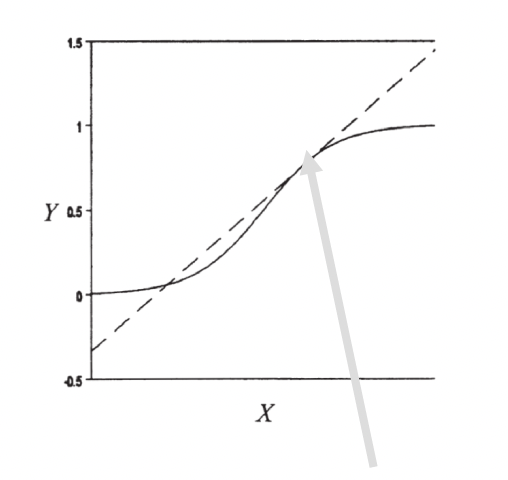
To get a marginal effect out of the margins command, you need to include dydx() to your margins command. That's that calculus terminology.

Now what makes the margins command difficult is that there are so so many options we can add to the command. Do we want to focus on one of our independent variables or two? Are we holding the other variables at means or at representative values? Are we working with continuous or categorical variables? This overview today is hopefully going to help you understand the grammar of this command and how to bend it to your will when you need to use it on your project.

There are four decisions you will need to make when producing margins. These four decisions form the basics of the many variations of the margins command. All of these examples will be from a logistic regression so they will be predicted probabilities or changes in probability.

To use the margins command, we need to run a regression first. This is the regression we'll be basing the following commands off of:

                                                logistic                  survived i.port i.female log_fare parch

Decision 1: Categorical or Continuous?

The first decision you will need to make when using margins, is what independent (X) variable to focus on. Remember, you as the analyst are using the margins or margins plot to visualize some finding, usually relating to a key independent variable in your analysis. For example, in our titanic analysis our key variable was port of boarding. With the margins command, the syntax for the command will change depending on whether your X variable of focus is categorical or continuous.

For a categorical variable, the variable name will be listed BEFORE the comma if other options are specified or don't include any comma at all.

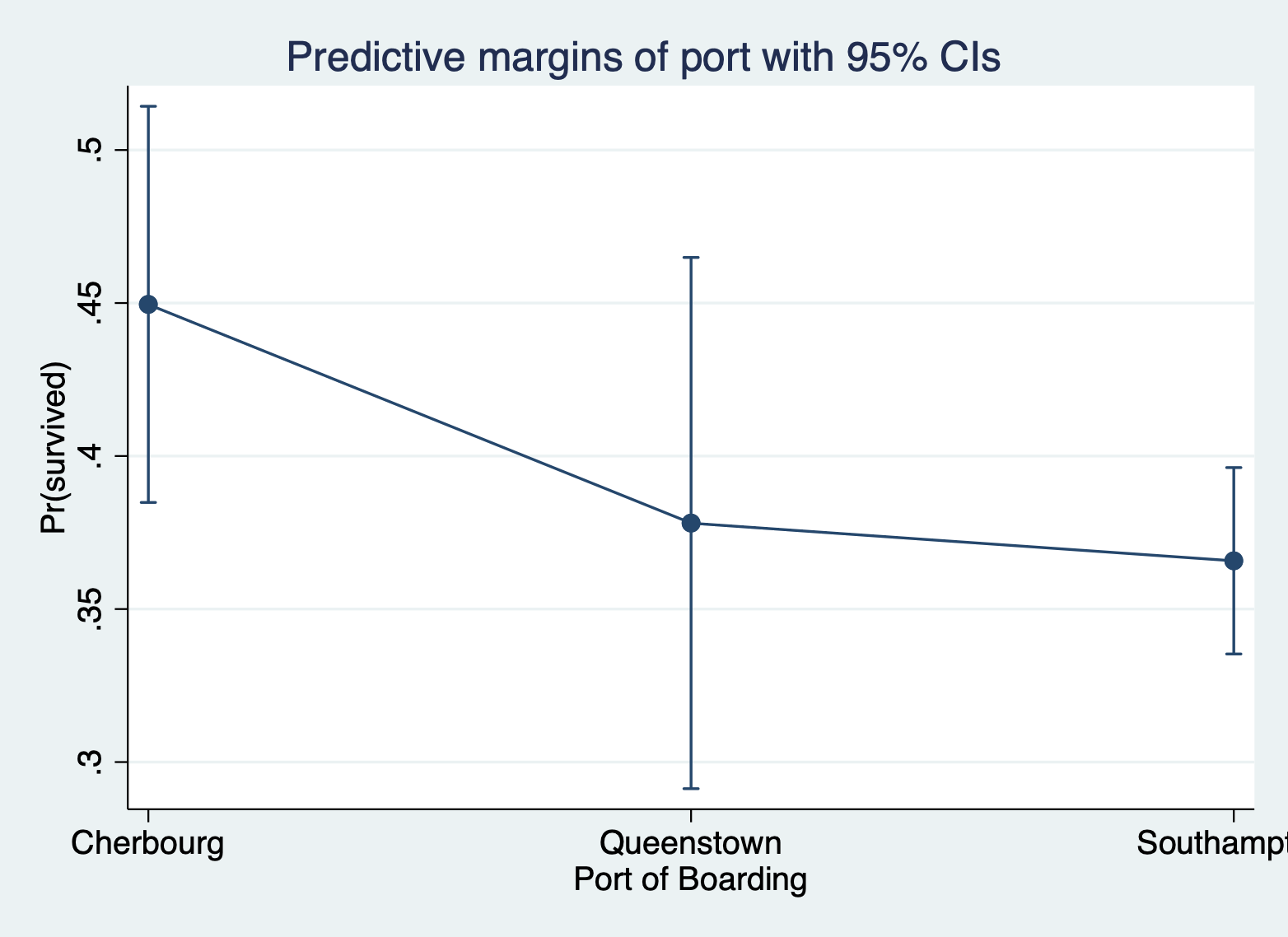
Here is the margins command and margins plot, focusing on port of entry.

For a continuous variable, the variable name will be listed AFTER the comma inside of an at() option statement and you must specify which values of X Stata should calculate/plot the margins for.

Here is the margins command and margins plot, focusing on ticket fare (logged to address skew).

                                  margins,                    at(log_fare = (0 2 4 6))                  marginsplot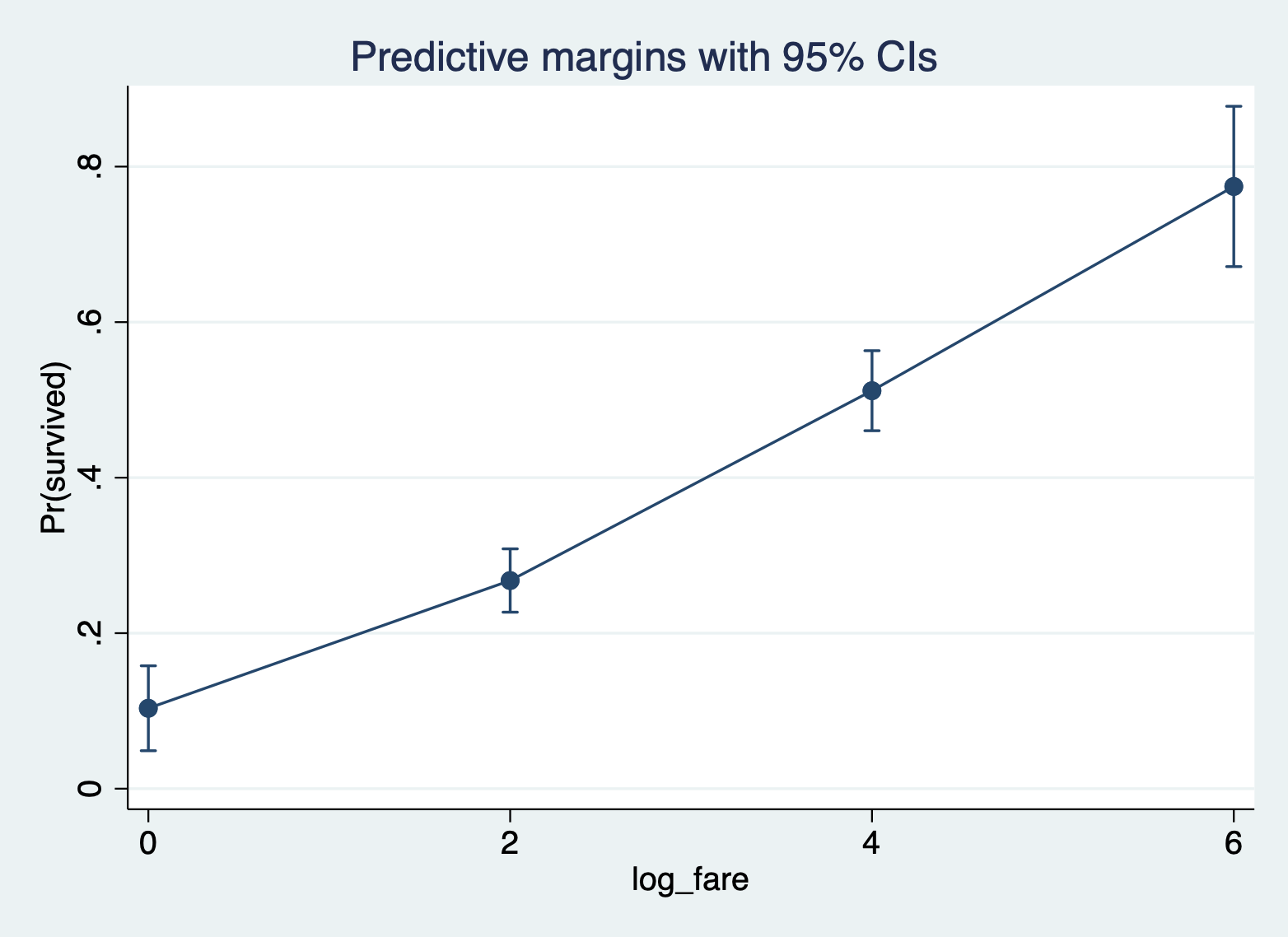

Decision 2: Add a second variable?

The second decision you will need to make is whether you want to add a second variable to focus on. Any more than two X variables of focus will lead to a complicated plot that doesn't communicate much to your reader. But adding a second variable can help you show not only the effect of your first variable, but how that effect varies across groups. It can illustrate interactions. Again, whether your variables are continuous or categorical will affect how you do this command.

Continuous and Continuous You will specify both variables AFTER the comma inside of the same at() and you must specify the multiple values of each variable to calculate/plot. The first variable will plot on the X axis and the second variable will be plotted as different lines.

Here is the margins command and margins plot for ticket fare and number of parents/children on board.

                                  margins,                    at(log_fare = (0 2 4 6) parch = (0 3 6))                  marginsplot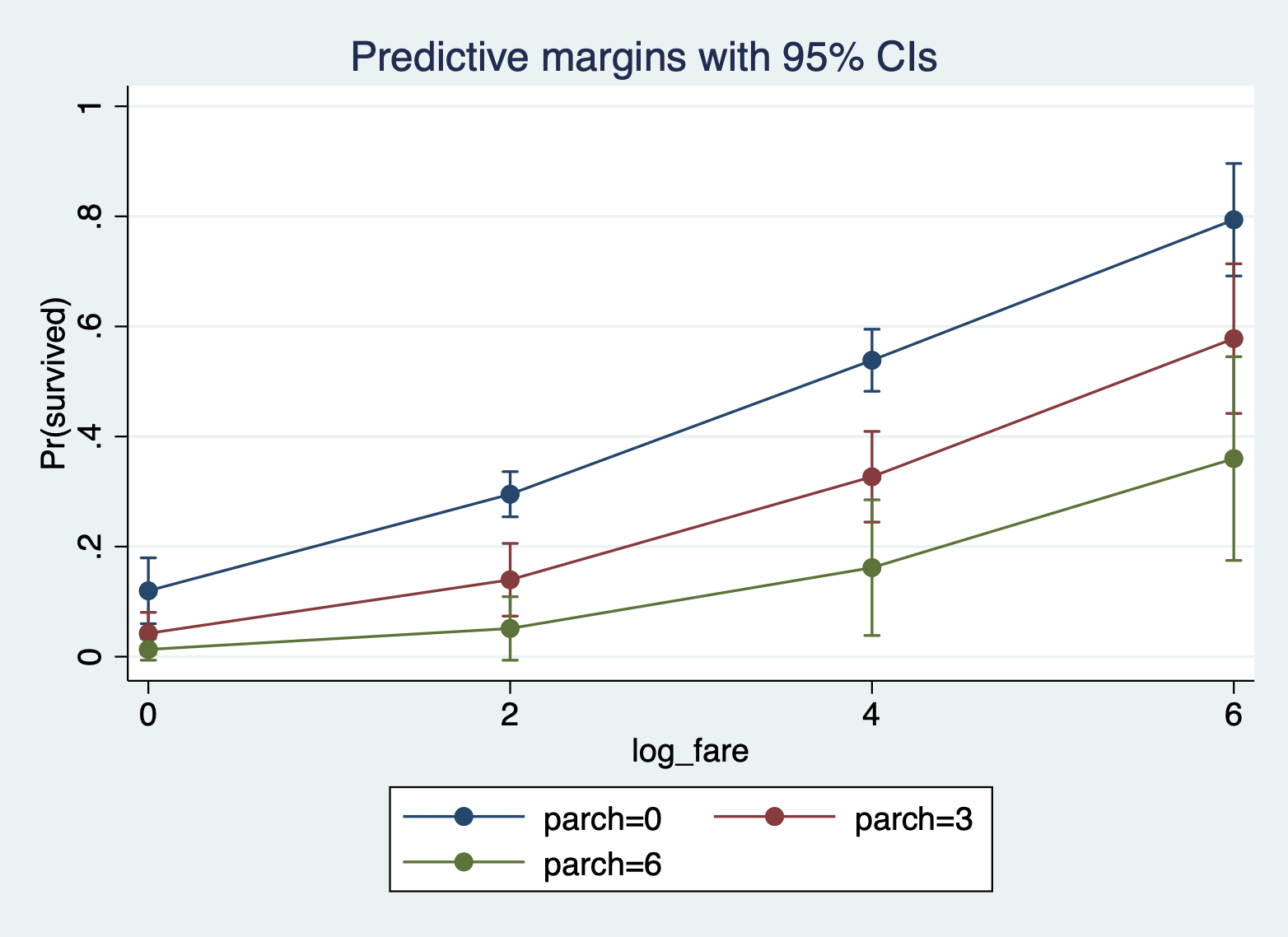

Continuous and Categorical You will specify the categorical variable BEFORE the comma and the continuous variable AFTER the comma within the at() option statement. If you only want to include certain categories, you can move the categorical variable into the at() statement and specify the categories to include.

Here is the margins command and margins plot for ticket fare and port of boarding.

                                  margins port,                    at(log_fare = (0 2 4 6))                  marginsplot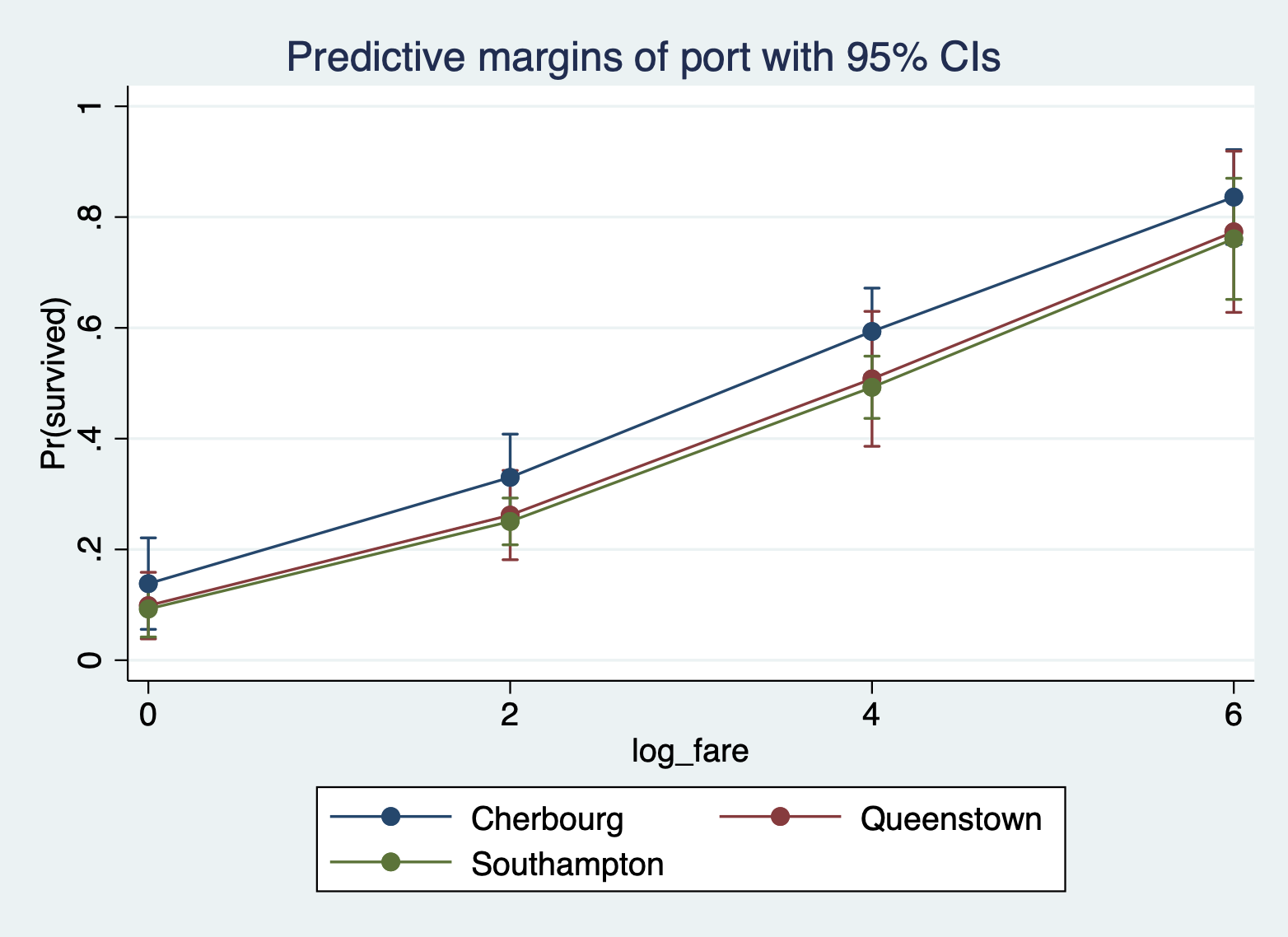

And here is the same plot, but with only Cherbourg and Queenstown.

                                  margins,                    at(log_fare = (0 2 4 6) port = (1 2))                  marginsplot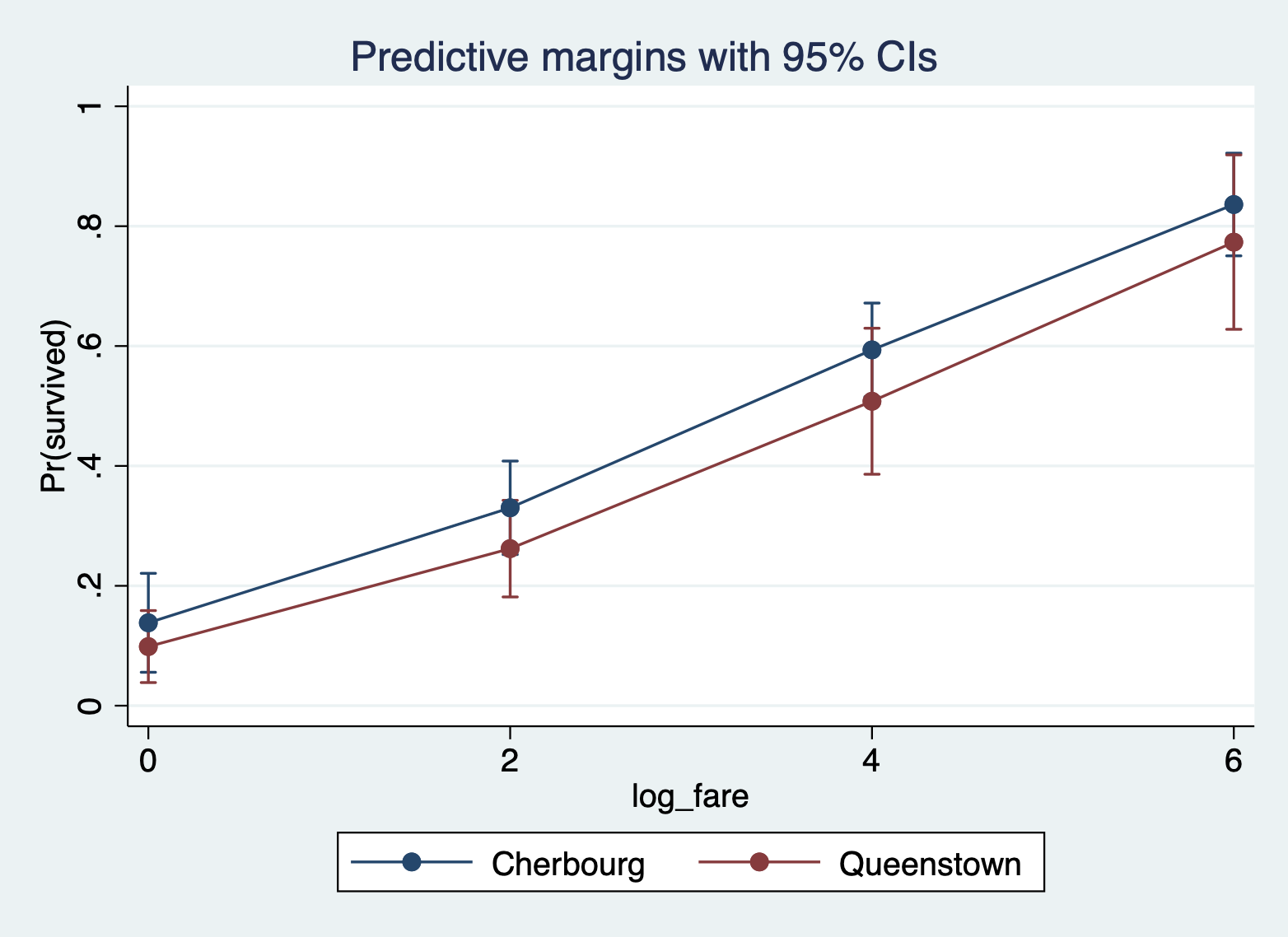

Categorical and Categorical You will specify the variable you want on the X axis BEFORE the comma and the variable you want split across different lines AFTER the comma in the over() optional statement.

Here is the margins command margins plot for port of boarding and sex of passenger with port on the X axis and sex as lines.

                                  margins port,                    over(female)                  marginsplot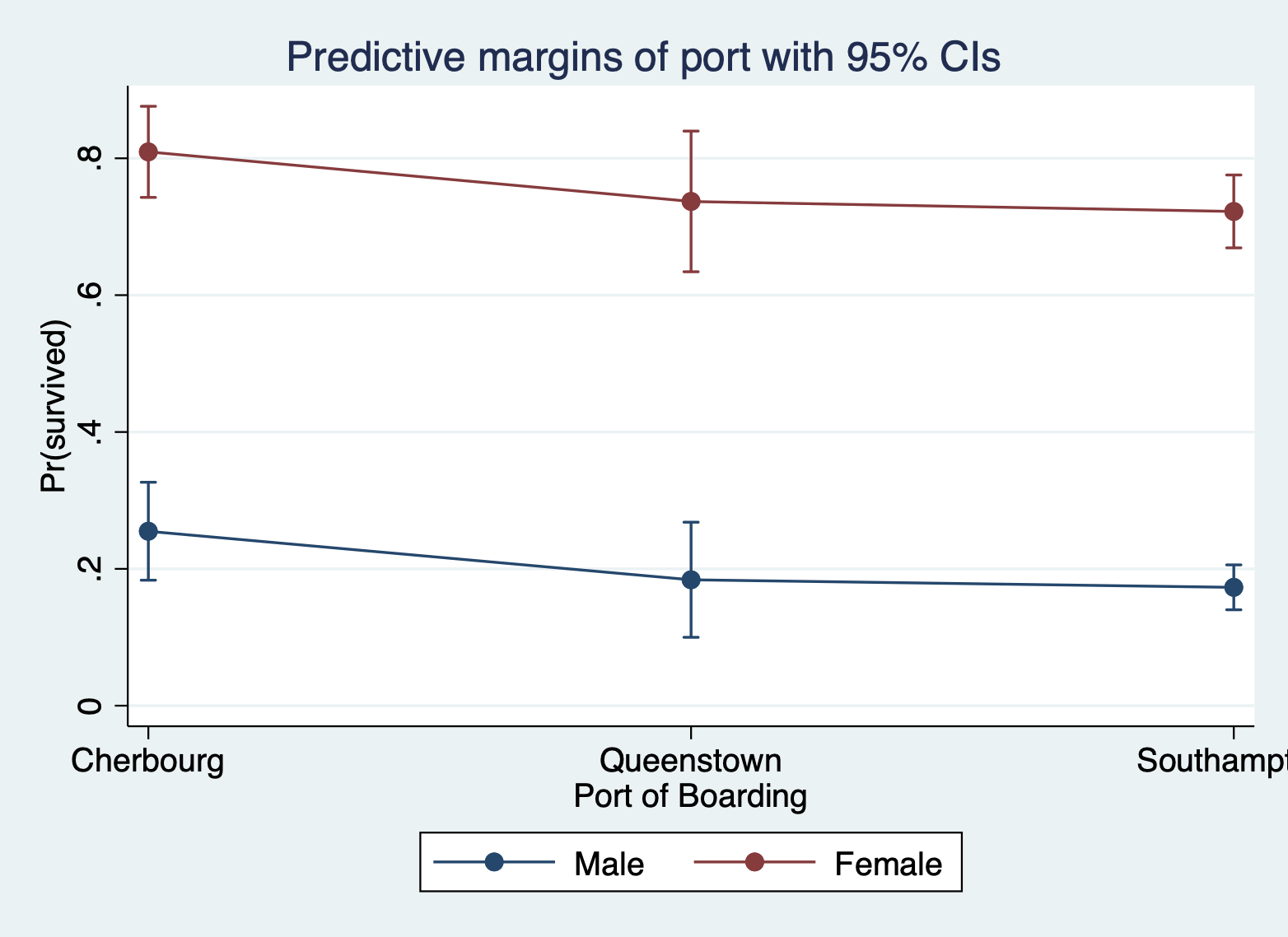

Decision 3: How will you handle the other X variables?

This is a review from last week. There are three approaches to handling the other X variables (aka the ones that are NOT the X variable you want to highlight):

  • Hold other variables AT MEANS
  • Hold other variables AT REPRESENTATIVE VALUES
  • Run everything with observed values and compute the AVERAGE predicted value/effect.

NOTE: For these I want you to note how the actual predicted values change, so I am not going to include the margins plot. Look at the actual calculated margins for each approach.

At means: You just have to add an at means after the comma

Here are the margins for port with the other variables at means.

              Adjusted predictions                                       Number of obs = 889 Model VCE: OIM  Expression: Pr(survived), predict() At: 1.port   = .1889764 (mean)     2.port   = .0866142 (mean)     3.port   = .7244094 (mean)     0.female = .6490439 (mean)     1.female = .3509561 (mean)     log_fare = 2.959024 (mean)     parch    = .3824522 (mean)  ------------------------------------------------------------------------------              |            Delta-method              |     Margin   std. err.      z    P>|z|     [95% conf. interval] -------------+----------------------------------------------------------------         port |   Cherbourg  |    .453225    .049525     9.15   0.000     .3561577    .5502923  Queenstown  |   .3466006   .0648861     5.34   0.000     .2194261    .4737751 Southampton  |   .3286141     .02262    14.53   0.000     .2842797    .3729486 ------------------------------------------------------------------------------

At representative values: You have to specify the specific values of the other variables within the at() option, but only ONE value per variable.

Here are the margins for port with the other variables at representative values.

                                  margins port,                    at(female = 1 log_fare = 2 parch = 2)                              
              Adjusted predictions                                       Number of obs = 889 Model VCE: OIM  Expression: Pr(survived), predict() At: female   = 1     log_fare = 2     parch    = 2  ------------------------------------------------------------------------------              |            Delta-method              |     Margin   std. err.      z    P>|z|     [95% conf. interval] -------------+----------------------------------------------------------------         port |   Cherbourg  |   .5240158   .0825546     6.35   0.000     .3622117    .6858199  Queenstown  |   .4133268   .0845754     4.89   0.000      .247562    .5790915 Southampton  |   .3939654   .0596048     6.61   0.000     .2771421    .5107888 ------------------------------------------------------------------------------

Average predicted values/marginal effects: Don't do a damn thing! This is the default.

Here are the average predicted probabilities for port of boarding.

              Predictive margins                                         Number of obs = 889 Model VCE: OIM  Expression: Pr(survived), predict()  ------------------------------------------------------------------------------              |            Delta-method              |     Margin   std. err.      z    P>|z|     [95% conf. interval] -------------+----------------------------------------------------------------         port |   Cherbourg  |   .4495649    .033027    13.61   0.000     .3848331    .5142967  Queenstown  |   .3781069   .0442857     8.54   0.000     .2913085    .4649054 Southampton  |   .3657791   .0155409    23.54   0.000     .3353196    .3962387 ------------------------------------------------------------------------------

Decision 4: Predicted values or Marginal effects

And finally, we can specify whether we want the predicted values or the marginal effects. All of the above examples were predicted values. Specifically they were predicted probabilities because we're working with logistic regression.

Predicted values: Again, don't do a damn thing! This is the default for the margins command.

Here again are the average predicted probabilities at different values of ticket fare (logged).

                                  margins,                    at(log_fare = (2 4 6))                                                
              Predictive margins                                         Number of obs = 889 Model VCE: OIM  Expression: Pr(survived), predict() 1._at: log_fare = 2 2._at: log_fare = 4 3._at: log_fare = 6  ------------------------------------------------------------------------------              |            Delta-method              |     Margin   std. err.      z    P>|z|     [95% conf. interval] -------------+----------------------------------------------------------------          _at |           1  |   .2676895   .0207842    12.88   0.000     .2269532    .3084257           2  |   .5118238   .0262607    19.49   0.000     .4603537    .5632939           3  |   .7744947   .0526051    14.72   0.000     .6713907    .8775987 ------------------------------------------------------------------------------

Marginal effects: When you do marginal effects, you move your variable of focus, regardless of whether it is categorical or continuous, AFTER the comma inside the dydx() option statement.

Here is the marginal effect for ticket fare (logged).

              Average marginal effects                                   Number of obs = 889 Model VCE: OIM  Expression: Pr(survived), predict() dy/dx wrt:  log_fare  ------------------------------------------------------------------------------              |            Delta-method              |      dy/dx   std. err.      z    P>|z|     [95% conf. interval] -------------+----------------------------------------------------------------     log_fare |   .1111977   .0158007     7.04   0.000     .0802289    .1421665 ------------------------------------------------------------------------------

You can get one marginal effect for a continuous variable OR get the marginal effects across the range if you so choose:

                                  margins,                    dydx(log_fare)                    at(log_fare = (2 4 6))                              
              Average marginal effects                                   Number of obs = 889 Model VCE: OIM  Expression: Pr(survived), predict() dy/dx wrt:  log_fare 1._at: log_fare = 2 2._at: log_fare = 4 3._at: log_fare = 6  ------------------------------------------------------------------------------              |            Delta-method              |      dy/dx   std. err.      z    P>|z|     [95% conf. interval] -------------+---------------------------------------------------------------- log_fare     |          _at |           1  |   .1043584   .0131838     7.92   0.000     .0785187    .1301981           2  |   .1365486   .0224777     6.07   0.000      .092493    .1806041           3  |   .1116513   .0047204    23.65   0.000     .1023996    .1209031 ------------------------------------------------------------------------------

Basics of Graphing Aesthetics

This lab will not review in detail all of the many different ways you can change the graphs you produce in Stata. However, I will provide you with this reference do file for graph formatting in Stata. It covers:

  • Titles, subtitles, and captions
  • Changing axis and tick mark options
  • Color of markers, lines, and the fill area
  • Style of markers and lines
  • Background colors for the plot area and graph area
  • Labelling specific values

Download formatref.do

Here is a resource just to learn more about adjusting plots with grstyle:
Download grstyle_StataGraphsMadeEasy.pdf

Good Graph Design

Example: A journal ready predicted values plot

Here is one example of a journal ready plot. This is code you can tweak and save to be your default style when producing plots for papers. I pulled this shortcut formatting from various places online, and it is in the reference .do file I put above.

We will use the grstyle shortcuts for changing the default settings for graphs. This is going to do the bulk of the formatting work for you, and would make your plot style consistent if you wanted to make several graphs for the same paper.

                                  * Install some helper commands (if                    you haven't already installed them)                                      net install http://www.stata-journal.com/software/sj18-3/gr0073/                                                        ssc                    install grstyle                                      ssc                    install palettes                                      ssc                    install colrspace                                    * Set the                    new                    default                    styles                    for                    your                    graph                                    grstyle                    clear                    // clear the grstyle settings                                                        set                    scheme                    s2color                    // sets the color scheme                                    grstyle init                    // initiates the gr style command                                    grstyle                    set                    plain, box                    // create a plain style, with a box around the plot                                                        * 'grid' is another good option you can play with                  grstyle                    color                    background                    white                    // turn the background white                                    grstyle                    set                    color                    mono                    // set a monochrome color scheme for points/lines                                                        grstyle                    set                    color                    Dark2, n(3)                    // set a color scheme for colored lines/points                                                        * other                    color                    schemes                    include                    Set1, Set2, RdYlGn, Dark1, Dark2                                      *                    I                    set                    the number                    of                    colors                    I                    need                    in                    the plot                    in                    ', n(3)'                  grstyle yesno draw_major_hgrid yes                    // include major grid lines                                    grstyle yesno draw_major_ygrid yes                    // include major grid lines                                    grstyle                    set                    legend                    10, box inside                    // move the legend inside the plot area                                                        *                    for                    this                    last                    command the number after                    legend                    refers to the corner                                                        *                    of                    the plot (1 to                    at                    least 12 like a clock).                    I                    wanted it                    in                    the                    upper                                                        * left.                    I                    just played around with numbers til                    I                    got it where                    I                    wanted.                  grstyle                    set                    size                    14pt: axis_title                    // change the size of axis text

I will calculate the margins quietly:

                                                      quietly                    margins,                    at(log_fare = (0 2 4 6) parch = (0 3 6))

And then here is the final plot. I don't have to change many options, because all the grstyle options I used above did that work. I left plot title blank, because often you will manually title plots in your manuscript. You can add a title in if you wish.

                                  marginsplot,                    ///                                                        title("")                    ///                                                                            ytitle("Predicted Probabilities")                    ///                                                        xtitle("Ticket Fare (logged)")                    ///                                                        legend                    (order(1                    "0 parents/children"                    2                    "3 parents/children"                    ///                                                        3                    "6 parents/children"))                                                                          graph                    export                    figs_output/probplot.png                    // save plot to your files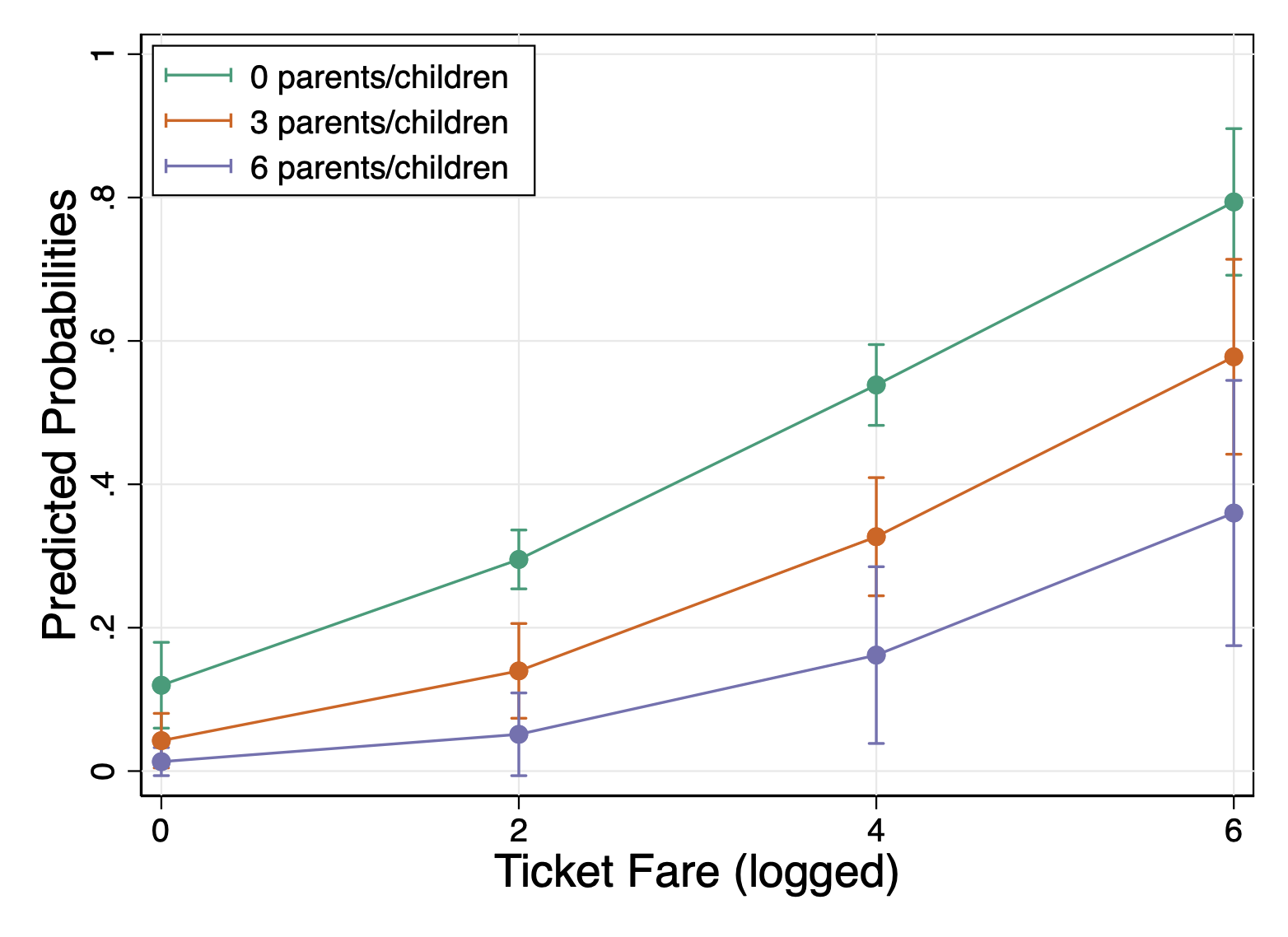

Here is a resource just to learn more about adjusting plots with grstyle:
Download grstyle_StataGraphsMadeEasy.pdf

Lab Assignment

From this logistic regression, produce a journal ready predicted probability plot with two X variables of focus (you can choose any two X variables from the regression). You can play around with grstyle or the direct commands from the reference file.